How It Will Work
In this post, I’ll outline the ideas I have so far as to the mechanisms that will hopefully allow this project to succeed.
Origins of the Original Idea
Originally, the idea for this project came to me in early April 2023, after a hyperbaric oxygen therapy session at the Vancouver General Hospital. I was talking with my dad about my hearing (or lack thereof hehe), and how I couldn’t tell which direction things were coming from, and though the details now escape me, we came to the topic of whether it was possible to deduce the direction of sound using a computer analogously to the way our brains do.
For a while, the idea lived far in the background of my mind, since I had IB exams in May to study for and focus on. Every once in a while, in a moment of boredom or distraction, I’d find myself thinking back to the idea, this challenge, and how it could be achieved.
The first approach I though of was something akin to triangulation, where by measuring the intensity of sound at different points, the source of the sound could be pinpointed.
How Triangulation Works
(click here to skip to next section)
Imagine you (top circle) and your friend (bottom circle) are soldiers in WW1, illustrated in purple, on your side of the front line (shown in red).
The enemy is firing artillery guns at you, but it’s dark and somewhat foggy, so no one can see where exactly the artillery is being fired from. However, every time a shell is shot, a flash lights up the sky, and a few seconds later, the shot is heard as a loud boom.
The enemy think they’re very clever hiding in the fog, but you and your friend have a clever idea: you measure how far you are from each other, let’s say in this case 500 meters. Then, next time you see a flash in the sky, you each count how many seconds it takes to reach you. After you hear the boom of the gun, you rush to meet each other, and take out a map.
Your friend counted 10 seconds before hearing the boom, and you counted 13 seconds. Light travels extremely fast (about 300 million meters per second \(\approx\) 1 billion kilometers per hour), so it covers the distance between the gun and you almost immediately; for practical purposes, we will assume it covers this distance instantaneously.
However, sound travels at a drastically slower speed of about 340 meters per second. Your friend counted 10 seconds between the flash and the boom, which means the sound travelled \(10\times340=3,400\textrm{m}=3.4\textrm{km}\) to reach your friend.
On you map, you and your friend draw a circle with a radius of \(3.4\textrm{km}\) on your map, with the center where your friend was standing:
You counted 13 seconds, so at \(340\textrm{m/s}\), you were about \(4.4\textrm{km}\) away; you draw another circle with this radius on your position.
If you only consider either of the single message, the enemy gun could be anywhere along the edge of the respective circle, which is a rather large arc of land. However, by considering both measurements, you know that the enemy gun must be at one of the intersection points of your circles. Since the enemy is, of course, across the front line and not behind you, the enemy gun (shown as an orange dot) must be at the intersection of the circles across the front line:
Applying this to Audio
How does this apply to this project?
Suppose you set up three microphones in a roughly equilateral triangle. For practical purposes, this triangle may have to be rather small, if it is to fit on a person’s body somehow, which makes measuring the delay between sounds rather difficult. However, perhaps due to the nature of the microphones and their orientation in space, or perhaps due to the way sounds tend to decay with distance, maybe it’s easier to detect changes in the mean intensity of the sound at each microphone.
Knowing this change of intensity, some calculations can be performed, and while the exact point of origin of the sound may not be accurately found, I think that the direction that the sound originates from should be simpler to find, and perhaps it may be found with higher accuracy than precise location.
This is the basis for how I’m approaching this project; perhaps my assumptions are flawed, and the intensity of sound is innacurate, or some other unforseen issue arises. In such a case I will re-evaluate possible approaches and come up with something new, but first I must test this theory.
A Conundrum and its Solution
A problem arises from this approach: what if there are multiple sources of sound?
Picture the following scenario. The three microphones are positioned in their equilateral triangle, and some processor is measuring the intensity of the sound signal of each microphone. With a single source emmiting a sound wave that decays as it travels, it is feasible that this setup could accurately estimate which direction the sound comes from based on the intensity of the sound signal at each mic:
The microphones, shown in red, are labelled based on the intensity of the signal they each pick up. Based only on these intensities, it would be reasonable to estimate the direction of the sound source to be somewhere within the “Direction Estimate” cone.
Now a second source of sound is added, emitting a different sound but at similar intensity (and with similar decay of intensity with distance):
The problem is that taking the same approach to estimate the direction sound is coming from would result in an estimate in between the separate sound sources, effectively pointing at the weighted mean position of all sound sources, where the weighting is the intensity of each sound.
This is not very useful for this project, as the idea is to enable spatial awareness by reporting all sounds in the vicinity (and their directons) to the user.
The way I plan to tackle this issue is by using a Fast Fourier Transform (FFT), which is a computational way to separate out a signal (in this case a sound signal) into its component frequencies (this video provdies a great intuitive explanation for how and why the fourier transform does what it does).
By taking the FFT of each incoming signal, whichever algorithm is used to estimate the direction of incoming sound can be applied to each detected frequency, allowing the direction of multiple sounds at once to be accurately estimated.
But why does the FFT Change Things?
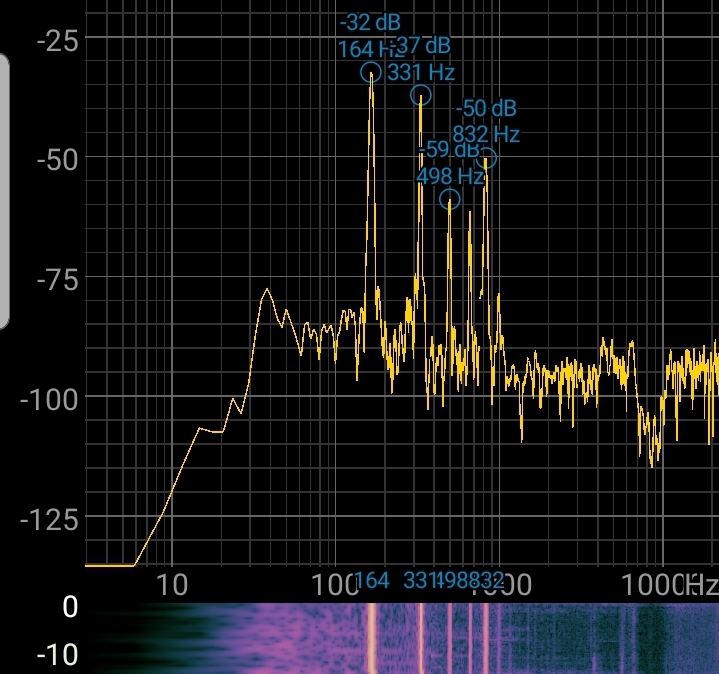
Sounds tend to have different makeups in terms of which frequencies are present in them, typically due to variations in pitch, i.e. which “note” the sound has, and the timbre, which is the character of the sound (what the sound sounds like). For example, you can have a car horn and a person’s voice create the same note, but they have distinct timbre, you can have multiple people talking at once (with similar tibre as voices tend to sound similar), but at different pitches.
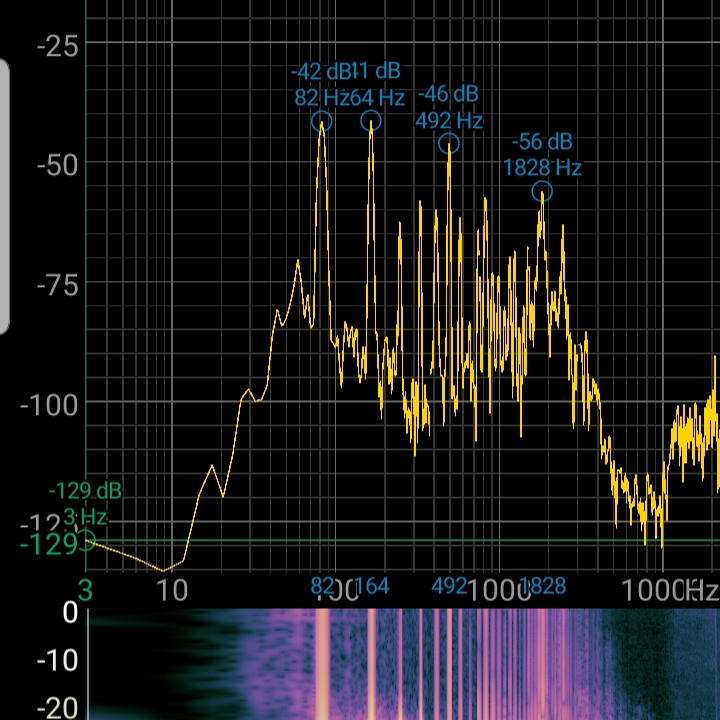
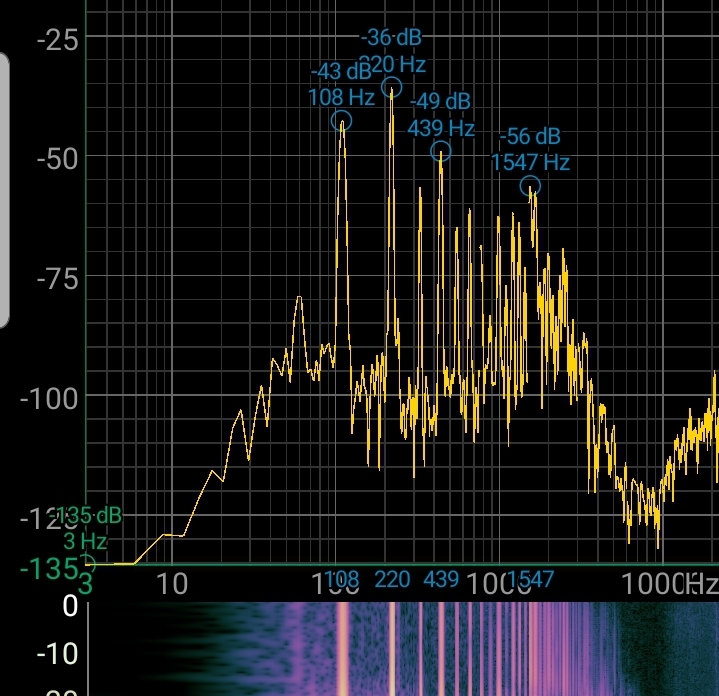
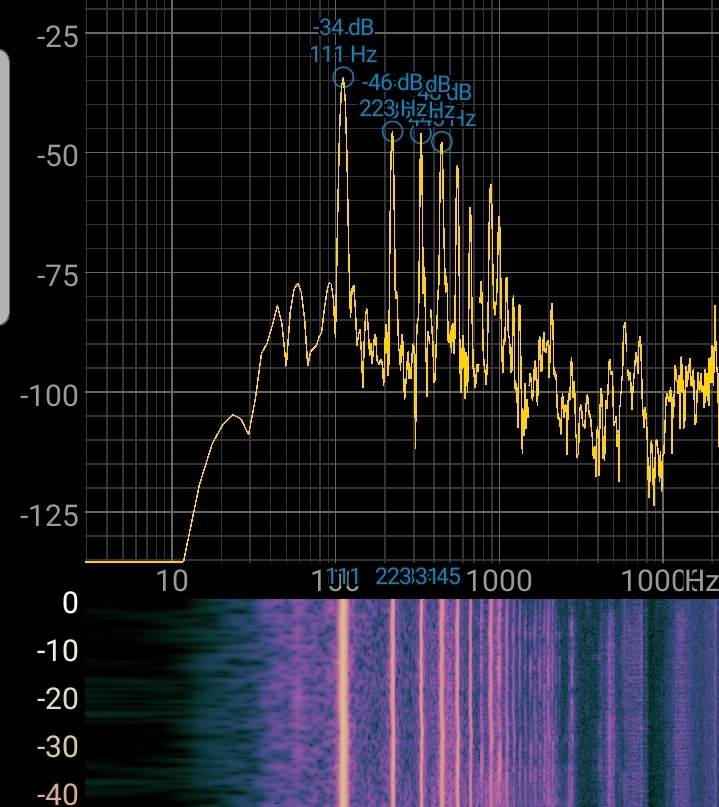
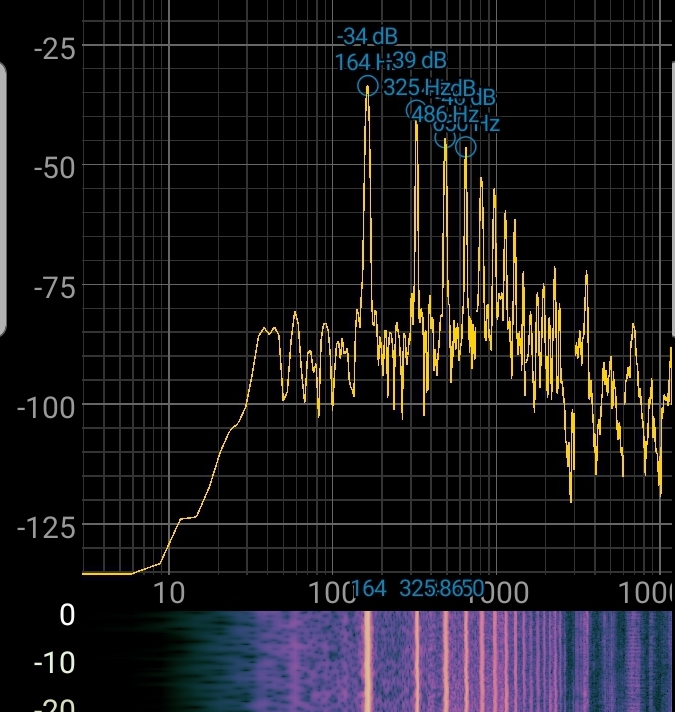
To illustrate the difference between these two, consider the following FFT plots of my keyboard’s piano sound and my voice; note that the horizontal axis is frequency in Hz, and the vertical axis is intensity in decibels.
The pitch of a sound is typically measured with its base (AKA lowest) frequency; check out how both A2s have almost the same base frequency, and hence are almost the same note (I sang the A a little bit sharp, i.e. a little too high).
Note some interesting similarities between these images:
- Both Keyboard notes have higher harmonic frequencies present than the voice FFT plots do. This is due to the difference in timbre between these sounds.
- Similarly, note the difference in the frequencies present between me singing an E3 with an “ahh” vs “ooh” vowel; the change in timbre is shown by the change in frequencies present (“aah” seems to have higher frequencies present).
If you choose any pair out of these FFT plots, there are almost always frequencies that are distinct to each sound. If the sounds have different pitch, then the base frequency, as well as most others, are shifted up or down, and can be distinguished due to this. If the sounds have different timbre, they have differently shaped fft plots with different frequencies present, although it’s true that many frequencies overlap.
Applying an FFT to a sound signal gives you the intensity of each frequency present in the sound, and in principle, with some processing, measuring intensity with multiple microphones should enable an estimate of the direction of that sound to be made.
So, picture taking the FFT of each of the three microphones in the above example multiple times per second, and instead of using the intensity of the audio signal as a whole, we can use the intensity of each component frequency to estimate in which direction each frequency is mainly coming from. Since most sounds you hear at a given moment tend to have unique pitch and timbre, this approach should enable the system to predict the direction of origin of multiple sounds at once.
Hopefully this approach successfully allows multiple sounds to be tracked simultaneously, but if it is ulitmately unsuccessful, other approaches such as using the phase of each frequency and directional microhpones will be explored.
 RC
RC